데이터분석 공부하기
추론통계(Inferential statistics) : 1) 확률과 모집단 추정 본문
추론통계(inferential statistics) : generalizing from a sample to a population
추론통계는 1) 모집단 추정(estimation), 2) 가설검정(testing hypothesis)으로 나뉜다.
Probability : 확률
- 확률의 개념
- 추론통계 분석방법의 토대 : 통계 검정에서 표본(조사대상의 일부)만 관측하고도 모집단(조사대상 전체)에 대한 결론을 내릴 수 있는 논리의 근거 (신뢰성/정확성 주장)
- 어떤 사건(event)이 일어날 확률 - 그 사건이 일어날 확실성(certainty)의 정도
- 베이지안 정리(Bayes theorem): 조건불 확률 개념을 발전시킨 이론; 표본자료로 모집단을 추론할 방법에 대한 이론
- '우연이라는 원칙으로 문제를 해결하려는 방법에 관한 논문'
- 과거에 일어난 일로 계산한 사전확률(prior probability)를 근거로 사후확률(posterior probability)를 산출할 수 있다
- 새로운 정보가 주어지면 수정하여 사후확률 다시 계산
- 확률분포(proabability distribution)
- 확률변수(random variable): 시행해 봐야 비로소 결과를 알 수 있는 변수; 취할 수 있는 값이 확률에 의해 정의되어 있는 변수
- 이산변수(discrete RV, ex-사람 수/개수; 확률 히스토그램), 연속변수(continuouse RV, ex- 키/몸무게) - 확률분포 : 확률변수X가 가질 값의 확률 분포 (확률변수의 어떤 값이 실현되기 쉬운지/어려운지 알 수 있다)
- A statistical function that describe all the possible values/likelihoods that a random variable can take - 확률밀도함수(probability density function) : 연속확률변수의 확률분포는 한 점 아닌, 어느 구간에 속할 확률로 정의하는데, 한 점에서의 상대적 가능성을 나타내는 확률밀도함수를 이용하여 정의함 (연속확률변수 - 키/ 강수량 등)
- 확률변수(random variable): 시행해 봐야 비로소 결과를 알 수 있는 변수; 취할 수 있는 값이 확률에 의해 정의되어 있는 변수
- 확률분포의 유형
- 이산확률분포(discrete probability distribution) : 확률 히스토그램; 베르누이분포, 이항분포, 포아송분포
- 연속확률분포(continuouse probability distribution) : 완만한 정규 곡선의 형태(이나 표본 데이터는 일부이므로 도수분포화하여 히스토그램으로 나타낼 수 밖에 없다); 균등분포, 지수분포, 정규분포
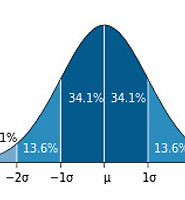
- 정규분포, 가우스분포(normal distribution, gaussian distribution): 평균 = μ, 표준편차 = σ
- 가장 대표적 분포: 1) 일상 측정의 대부분은 정규분포를 따름, 2) 모수추정에 필요한 정규성 준수
- ±1σ (68%), ±2σ(95%), ±3σ(99%), 그 이상은 무한대로 점근/축과는 만나지 않음 (asymptotic, ♾)
- 표준정규분포, Z-분포 (standard normal distribution, z-distribution) : 평균 = 0, 표준편차 = 1
- 서로 다른 크기의 변량을 가진 변수들의 객관적 비교를 위해 표준화한 방법
- 각 변량(variance)에 대한 확률값을 구하는데 많이 이용 : 확률밀도함수개념으로 z table을 사용하여 계산(유의성 검증)
z-score = (x-μ)/s

출처: biochemia medica
참고: 확률변수와 확률분포 (https://www.youtube.com/watch?v=JjX4EPhfUps)
모집단 추정(estimation) : 표본이 모집단을 잘 대표하는가?
- 표본데이터로 모델을 만들어 일반적인 예측/추론을 만들기 위해서는 표본이 모집단을 잘 대표해야한다(정확한 모집단 추론)
- 추론통계에서 모집단에 대한 추정을 위해 표본으로 얼마나 모집단을 정확히 알 수 있는지 알아야한다.
그러므로, 표본 개별데이터가 아닌, 표본에 대한 모집단 대표성을 알 수 있는 표집분포, 표준오차, 신뢰도를 사용한다.
- 표집분포(sampling distribution) : N이 같은 여러 표본 그룹들의 각 평균을 도수분포로 나타낸 것
- 표집변동(sampling variation) : 여러 표본을 표집했을 때 표본들 사이에서 각 평균의 차이가 있는 것
- 중심극한정리(central limit theorem, CLT): N이 클수록 표본평균은 가운데로 모이며(모평균) 표본평균의 변의성(표준오차) 감소
- 종류 : mean, proportion, t-sampling distribution(N은 표본 그룹의 갯수가 아닌 그룹 내 데이터 갯수) - 표준오차(standard error of the mean, SEM): 모평균으로 부터 표본평균들이 표준적으로 얼마나 떨어져 있나?
표본평균의 표준편차: SE = σ/(√n)- 신뢰구간 산출: 신뢰구간은 동일 N 표본을 100차례 임의 추출 시, 각 표본의 신뢰구간을 산출했을 때, 95개는 모평균을 포함한다는 것을 의미 -> 실제로는 하나의 표본밖에 없으므로, 표본평균+구간(x̅ ± d)이 된다(모수를 포함할 수도 안포함할 수도). 그러므로, 표집분포 모양이 퍼져있어(작은 N) 표준오차가 크면 모평균 포함을 가정해야할 각 표본의 신뢰구간이 커지고, 작으면 신뢰구간도 작아진다.
- 표본이 모집단을 대표하는 정도 : 표준오차가 작을 수록, 가운데로 모이는 분포가 되며 (알 수 없는)모평균이 가운데 있을 확률이 높아지므로 더 정확히 모평균을 추정할 수 있다(신뢰구간이 작음). SEM은 모평균 추정에 대한 불확실성을 나타냄
- 유의성 검증에 활용 : (*모집단을 알 수 없기에 추론)
- 동일 모집단 : 표준오차('일반적으로 표본의 평균들은 이만큼 떨어져있다')로 같은 모집단에서 추출한 두 표본 평균이 얼마나 '합리적이게' 떨어져있을 수 있는지 결정; 표준오차가 크면, 두 평균이 크게 떨어져있어도 동일 모집단에서 추출했다고 봄(유의미X)
- 다른 모집단 : 표준오차를 기반으로 두 표본 평균이 너무 떨어져있는 경우 (확률 5%이하) 서로 다른 모집단에서 추출됐다고 봄;
다른 모집단이란, 실험 조건 조작으로 서로 다른 모집단이 된 경우 예) t-test: t = z/SE
- 신뢰구간 : 표준오차를 사용해 신뢰구간의 상하계를 구하므로 SEM이 높으면 신뢰구간이 넓어져 유의할 확률이 적어진다.
또한, 넓은 구간으로 타당도/신뢰도도 감소한다. SEM이 낮으면 (N이 큰 경우 등) 어떤 효과가 있을 때 효과가 나타다는 정도가 더 뚜렷하게 가운데(평균)로 몰리기에 신뢰구간이 감소하고 유의할 확률이 증가하며, 타당도/신뢰도가 증가한다.
참고: https://www.scribbr.com/statistics/standard-error/
The standard error is used in hypothesis testing regarding whether or not two or more means are drawn from the same population (i.e., equal to each other) or different populations (i.e., they are different from each other). The standard error tells you how much, more or less on average, one mean is going to vary from another mean when they come from the *same* distribution."What is typically done in hypothesis testing is to compare the differences between the means relative to the standard error of the mean and then decide, based on the size of that difference, whether or not the means are from the same or different populations. So, the standard error’s role is to estimate how much, on average, some mean should change from sample to sample just by chance. You can use the standard error to calculate other statistics, such as t, to determine the probability of observing your result when the “null hypothesis” (no difference) is assumed to be true. When that probability is less than some acceptable chance of making an error (a type 1 error), i.e., when that probability is less than “alpha” we tend to reject the null hypothesis.
출처 : https://www.quora.com/What-is-the-role-of-a-standard-error-in-the-testing-of-hypothesis
- 신뢰구간(confidence interval, CI) : 모집단의 값이 속하리라고 간주되는 값의 범위(x̅ ± d)
- 참고: https://www.youtube.com/watch?v=TqOeMYtOc1w
- 신뢰구간 추정의 유형 : 모평균, 모비율, 모분산
- 신뢰구간 & 가설검증(모평균, 유의미): 95% CI = x̅ ± 2 SE (margin of error, ME = 2 * SE)
- 표준오차(표본 평균들이 합리적이게 떨어져 있을 수 있는 정도)를 기준으로 각 표본 평균들의 신뢰구간(상하계)를 계산한다.
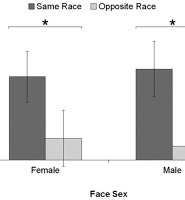
- 신뢰구간 가시화 : 신뢰구간을 오차막대(error bar)로 표시("𝖨"), 두 그룹간 차이를 잘 보여줌
- Accept H₀ : 오차막대가 곂치는 경우 (표본들이 합리적이게 떨어져있을 수 있는 범위 내 서로 위치한다)
동일 모집단에서 추출됐을 가능성이 크다 (μ₁ = μ₂ or μ = x̅ , no difference)
- Reject H₁ : 오차막대가 거이 곂치지 않는 경우 (ex- 95%CI의 경우 5%미만 overlap)
1) 다른 모집단에서 추출(다른 모평균 포함), 2) 동일 모집단이나, 하나는 모집단 평균 포함 X (100개 중 5개)
5% is unlikely-> 다른 모집단에서 추출했을 가능성이 높다;
두개의 무작위 표본(동일 모집단)에서 조건 조작으로 변화(서로 다른 모집단이 되다, μ₁ ≠ μ₂ or μ ≠ x̅ , sig. difference)
- N이 작으면, 겹칠 수 있는 구간이 넓어지므로 확률이 올라가고 유의하지 않다고 나올 수 있다/ 신뢰도/타당도도 낮음
- 모평균 신뢰구간 산출 방법(CI 상계/하계 산출):
-모분산이 알려진 경우 : 정규분포 or n>30 (중심극한정리에 따른 정규분포 전제)
- 표준정규분포(Z)로 d(신뢰구간) 산출 :
신뢰구간의 상/하계(upper/lower bound) = x̅ ± (z₍₍₁₋𝑝₎,₂₎ x SE)
-공식 유도 : z-score공식(z = (x -x̅)/ s)
1) z = (x -x̅)/ SE (관측값들의 변이성이 아니라 표본평균의 변이성에 관심)
2) x = (z * SE) + x̅
3) 신뢰수준 별 z-score(95%) : 1-p(신뢰구간의 확률) = (1- 0.95)/2 = 0.025(2.5%)
=> 2.5%에 대한 z값 = 1.96 (z분포표 참고)
4) x̅ ± (1.96 x SE)
- 모분산이 알려지지 않은 경우 : n <30일때, 모분산대신 표본 분산추정량(s)를 사용 -> t 분포로 신뢰구간 추정
- t 분포 : 표본 크기가 커짐에 따라, 형태가 변하는 확률 분포 (n>30는 정규분포와 거이 같다)
신뢰구간의 상/하계 = x̅ ± (t 𝑛₋₁ x SE) *n-1는 자유도(df: 자유롭게 변할 수 있는 변수의 수)
출처 및 참고 : '앤디 필드의 유쾌한 R 통계학'
- 신뢰구간 & 가설검증(모평균, 유의미): 95% CI = x̅ ± 2 SE (margin of error, ME = 2 * SE)
'통계' 카테고리의 다른 글
| R - graph(ggplot2) (0) | 2022.01.13 |
|---|---|
| R- Rstudio in Mas OC (0) | 2022.01.03 |
| 추론통계(Inferential statistics) : 2) 통계모형과 가설검정 (0) | 2021.12.30 |
| 기술통계(descriptive statistics) (0) | 2021.12.28 |
| 기초 연구방법론 (0) | 2021.12.27 |